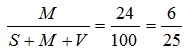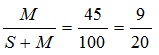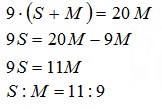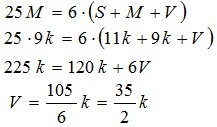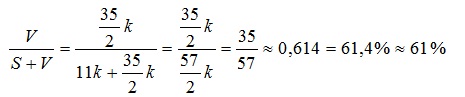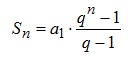Решење десетог недељног задатка – Олимпијски поредак

    Уколико су Мина и Макс у истој колони, онда је Мина старија од Макса, јер је Мина најстарија у тој колони.

    Ако су Мина и Макс у истој врсти, и онда је Мина старија од Макса, јер је Макс најмлађи у тој врсти.

    Ако су Мина и Макс у различитим колонама и врстама, онда постоји трећа особа, назовимо је Средоје, која је у истој колони као Мина и у истој врсти као Макс. Како је Мина старија од Средоја – јер су у истој колони (у којој је Мина најстарија), и како је Средоје старији од Макса – јер су у истој врсти (у којој је Макс најмлађи), закључујемо да је Мина и у овом случају старија од Макса.

    Дакле, може се утврдити да је Мина сигурно старија од Макса.

Решење деветог недељног задатка – Бодовање на такмичењу

    Будући да два најлакша задатка носе заједно 10 бодова, а како сваки задатак носи различит број бодова, закључујемо да тежи од њих носи најмање 6 бодова. Са друге стране, два најтежа задатка носе заједно 18 бодова, па лакши од њих носи највише 8 бодова.

    Дакле, средњи по тежини задатак мора да носи 7 бодова, а на основу тога следи да је такмичар који је тачно урадио свих 5 задатака имао 10 + 7 + 18 = 35 бодова.

    Такође, можемо закључити да су задаци идући од најлакшег до најтежег носили редом 4, 6, 7, 8 и 10 бодова.

Решење осмог недељног задатка – Зачарана мочвара

    На основу услова задатка приметимо да на крају може опстати само једна врста. Како после сваког једења парност броја рода и скакаваца остаје различит, закључујемо да на крају не могу остати само жабе. Такође, после сваког једења парност броја рода и жаба остаје различит, па не могу остати само скакавци. Дакле, могу остати само роде. При томе, да би нестале све жабе, мора бити бар 55 једења, при којима се укупан број животиња смањује за 55, па највише могу остати 23 животиње.

    Заиста, ако 17 жаба најпре поједе све скакавце, остаће 23 роде и 38 жаба. Нека надаље, кад год рода поједе жабу, једна жаба поједе насталог скакавца. Тако ће број рода остајати исти, а број жаба ће се после сваког оваквог пара једења смањивати за 2. Након 19 понављања овог поступка (то јест укупно 17 + 38 = 55 једења), неће више бити жаба и остаће тачно 23 роде, што je на основу доказа из првог дела решења и највећи број животиња које могу опстати.

Решење шестог недељног задатка – Срећни разломци

    Проширимо сваки од разломака 7/9 и 8/9 редом бројевима 2, 3, 4, …, 8. Сваки разломак који се налази између овог пара разломака проширеног одговарајућим бројем, већи је од 7/9, а мањи од 8/9. Да би такав разломак задовољио и други услов задатка – да буде срећан разломак, требало би да је сводљив, тако да после скраћивања постане разломак са једноцифреним имениоцем.

    Размотримо сада сваки од појединачних случајева:

• Проширивањем са 2, добија се пар разломака 14/18 и 16/18. Између њих је разломак 15/18 = 5/6, који задовољава услов задатка.
• Проширивањем са 3, добија се пар разломака 21/27 и 24/27. Између њих су разломци 22/27 и 23/27, али оба ова разломка су несводљива.
• Проширивањем са 4, добија се пар разломака 28/36 и 32/36. Између њих су разломци 29/36, 30/36 и 31/36; само се разломак 30/36 може скратити, то јест 30/36 = 5/6, а овај разломак је већ откривен.
• Проширивањем са 5, добија се пар разломака 35/45 и 40/45. Између њих су четири разломка са истим имениоцем 45, од којих је могуће скратити два (36/45 и 39/45), а само један задовољава услов задатка 36/45 = 4/5.
• Проширивањем са 6, добија се пар разломака 42/54 и 48/54. Између њих je само један разломак са имениоцем 54 који после скраћивања има једноцифрен именилац – то је 45/54 = 5/6, а овај разломак је већ раније пронађен.
• Од шест разломака који се налазе између 49/63 и 56/63 (добијених проширивањем почетних разломака са 7), само разломак 54/63 = 6/7 задовољава услове задатка.
• Постоје два разломка са имениоцем 72, од укупно седам који се налазе између бројева 56/72 и 64/72, а који испуњавају услов да после скраћивања постају срећни разломци. То су 60/72 = 5/6 (већ нађен) и 63/72 = 7/8.

    Проширивање почетних разломака са 9, 10,… не би дало нове разломке који би задовољили услове задатка.

    Дакле, између 7/9 и 8/9 постоје тачно четири срећна разломка: 4/5 , 5/6, 6/7 и 7/8.

Решење петог недељног задатка – Квалитет сира

    Означимо са S садржај суве безмасне материје, M садржај млечне масти и V садржај воде у сиру. Према условима задатка важи следеће:

и

    Из друге од ових једнакости следи

 па можемо изразити S=11k и M=9k.

    Применом добијеног резултата у првој једнакости, биће

    Сада је:

    Дакле, садржај воде у безмасној материји овог сира, заокружен на цео број процената, износи 61%. Према члану 36. Правилника о квалитету производа од млека и стартер култура (Сл. гласник РС бр. 33/2010), овај сир је класификован као полутврд сир.

Решење четвртог недељног задатка – Млади математичари

Наредном табелом дате су све изречене тврдње такмичара, док је у индексу сваке означене тврдње написан иницијал такмичара који је ту тврдњу изрекао.

    Претпоставимо да је истинит Катаринин исказ да Саша живи у Новом Саду. Онда је неистинита друга Катаринина тврдња да је она из Ниша, што је уједно и Јеленина тврдња. То управо значи да је тачан други Јеленин исказ – да је она из Новог Сада, а то доводи до контрадикције, јер су тада и Саша и Јелена из Новог Сада. Овај случај је приказан следећом табелом.

    Дакле, претходна претпоставка је била погрешна, што значи да Саша не живи у Новом Саду, па је истинит други Катаринин (уједно и Јеленин) исказ да је Катарина из Ниша. То повлачи даље да је нетачна Бранкова тврдња да је Катарина из Чачка, па је истина да је Бранко из Новог Сада. Ово даље имплицира да је лажан Оливерин исказ да је Бранко из Ужица, па је истинита њена друга изјава да је Јелена из Чачка. Даље следи да Јелена није из Ужица, па је Саша из Врања. На крају је остала „нераспоређена“ Оливера, па како су сви из различитих градова, закључујемо да је она из Ужица. Читав поступак је приказан табелом која следи.

    Коначно долазимо до решења задатка: Бранко је из Новог Сада, Јелена из Чачка, Катарина из Ниша, Оливера из Ужица и Саша из Врања.

Решење трећег недељног задатка – Стабло живота

    У стаблу нашег живота, у првој генерацији имамо 2 претка – родитеље, у другој генерацији 4=2² – наше бабе и деде, а у трећој генерацији 8=2³ – то су наше прабабе и прадеде. Вратимо ли се још мало кроз време, скуп наших директних предака почиње нагло да расте, у овом случају експоненцијално. Већ у осмој генерацији биће ту њих 256, док се у двадесетој генерацији број људи који су се размножавали у корист сваког од нас попео на невероватних 1.048.576 жена и мушкараца.

    Дакле, свака генерација наших предака представља један члан геометријског низа чији је први члан 2, а количник два узастопна члана такође 2. На основу овога закључујемо да је укупан број наших директних предака до n-те генерације сума S_n свих чланова поменутог низа

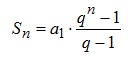то јест

    Најмањи природан број који је решење ове неједначине је n=36. (Ученици који не познају особине геометријског низа могли су „пешачком“ методом да дођу до овог резултата.)

     Дакле, укупан број директних предака сваког од нас, већ са 36. генерацијом превазилази укупан број људи који су икада живели на Земљи. Претпоставимо ли, врло произвољно, да су се у једном веку рађале 4 генерације наших предака, долазимо до запањујућег резултата да број наших директних предака који су живели у последњих 9 векова превазилази укупан број људи који су икада живели на Земљи.

    Како је то могуће? Очигледно да је у неком од наших закључака грешка! Одговор је прост: Наша линија није тако чиста! Не би нас било без мало инцеста, у ствари без прилично инцеста, мада на генетски дискретној удаљености. Са толико милиона предака сигурно је било много прилика да нам је неки далеки предак са мајчине стране уједно и предак по очевој линији. Штавише, обазремо ли се око себе у аутобусу, школи, парку, ресторану или ма ком другом посећеном месту, већина људи које видимо, а који припадају нашој раси и земљи, вероватно су нам неки даљи рођаци. У прилог овој тврдњи иде и чињеница да ако упоредимо своје гене са генима ма ког другог човека, биће 99,9% исти. То нас и чини једном врстом. Малене разлике у тих 0,1% – „отприлике једна нуклеотидна база у сваких хиљаду“, да цитирамо британског генетичара Џона Салстона, јесу оно што нам даје индивидуалност.

    Па када вам се неко следећи пут похвали да је потомак Константина Великог, Немањића или цара Лазара, требало би да сместа одговорите: „И ја!“. У најбуквалнијем и најфундаменталнијем смислу, сви смо једна породица.

Решење другог недељног задатка – Преварени продавац

    Продавац није у праву. Он је изгубио само 50 динара.

    Заиста, да је новчаница од 50 динара била права, продавац не би био на губитку. Међутим, како је од купца добио лажну новчаницу од 50 динара, дао му оловку од 18 динара и вратио кусур од 32 динара, продавац је на губитку свега 50 динара, тј. 18 динара + 32 динара (вредност оловке + кусур).

Решење првог недељног задатка – Ручак професора Косте Вујића

    Из загонетне приче професора Косте Вујића закључујемо да два узастопна месеца почињу недељом, јер се прва недеља ни у једном од ових месеци не поклапа са недељом после прве суботе у месецу. Дакле, први од ових узастопних месеци мора имати цео број седмица. Једини такав месец је фебруар просте године (28 дана).

    Овим је први део задатка решен: професор Вујић је код „Српске круне“ ручао 1. фебруара, а затим 8. фебруара код „Коларца“, 1. марта код „Руског цара“ и коначно 8. марта у „Касини“ на Теразијама.

     Михаило Петровић Алас је у овој причи већ професор Велике школе у Београду, а он је то постао 1894. године. Са друге стране, професор Коста Вујић је живео до 1909. године. То значи да се ова прича дешава просте године између 1894. и 1909. године, у којој је 1. фебруар била недеља. Увидом у календаре из тог периода закључујемо да све постављене услове испуњава једино 1903. година.

    Дакле, наша прича се одиграва управо те, просте, 1903. године.